If you are interested in information geometry and how it underlines all our thinking about models as an alternative to ANN-based AI, skip to Information Geometry 101. Otherwise, read ahead to see our published studies on coagulation and HIV.
The Coagulation Cascade: Information Geometry in your blood, stream-lined
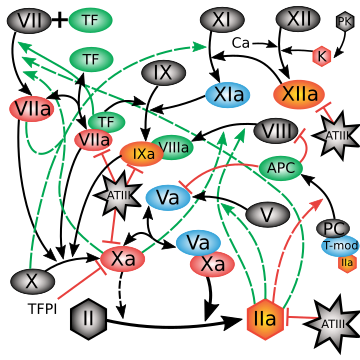
The coagulation cascade is one of the best-characterized signaling systems in human physiology, and also one of the most daunting to model quantitatively. In response to tissue injury, two distinct initiating branches--activation of Factor VII (the extrinsic pathway) and Factor XII (the intrinsic pathway)--converge on the generation of thrombin (Factor IIa), which in turn cleaves fibrinogen to fibrin, forming a blood clot. These processes are mediated by a densely interwoven network of enzymes, cofactors, and feedback loops that span molecular to physiological scales. The biological richness that makes coagulation a central case study in quantitative systems pharmacology (QSP) also makes it a notorious challenge: nonlinear kinetics, overlapping pathways, and therapeutic relevance (as the target of most anticoagulants) mean that models must be both detailed and predictive across a wide range of conditions.
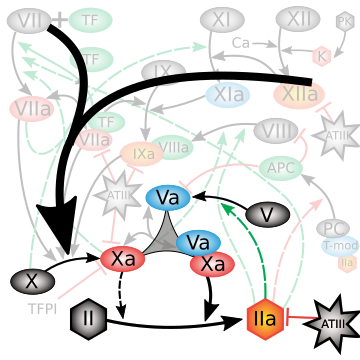
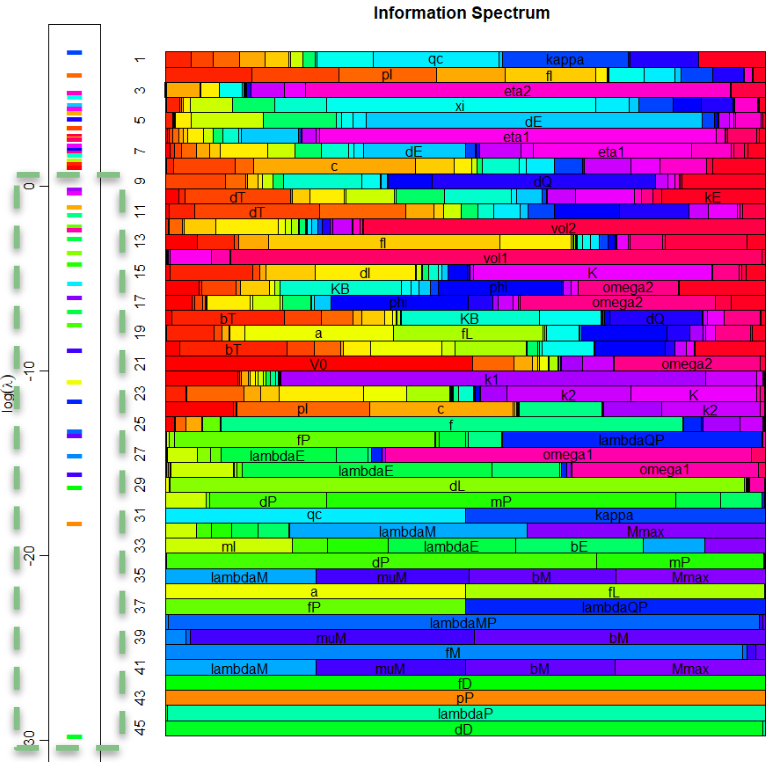
Nayak and colleagues (2015) approached this challenge with a comprehensive mechanistic model that encoded dozens of reactions and parameters derived from the literature, calibrated to thrombin generation profiles. While powerful, the model suffered from the classic problem of "too many knobs": most parameters could not be uniquely identified from available data, and brute-force simulation exposed instability across solvers. This is where information geometry (IG) enters. By analyzing the Fisher Information Matrix (FIM), IG methods revealed a sharply anisotropic parameter space: only a handful of combinations of parameters governed the observable thrombin responses, while the rest resided in flat, sloppy directions with negligible effect. This eigenvalue spectrum (see figure at right) made the dimensionality reduction explicit, providing principled guidance on how to collapse the original network into a minimal yet mechanistically faithful core.
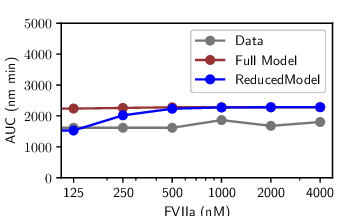
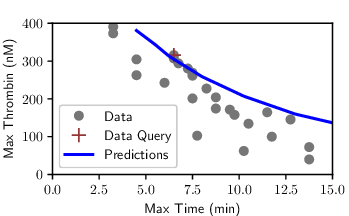
The reduction distilled the cascade into a model with just a small set of parameters and five dynamical variables, with Factor IIa-mediated activation of Factor V emerging as the critical feed-forward loop. Despite the radical compression, the model retained remarkable predictive power: fitting to a single thrombin generation profile enabled it to forecast time to peak, peak level, and area under the curve for 27 other experimental conditions with accuracy rivaling the full model (see figures at left). Equally important, the streamlined equations eliminated solver instabilities and cut computation time by two orders of magnitude, turning an unwieldy benchmark into a nimble predictive tool. In short, the IG-guided reduction did more than simplify; it illuminated the mechanism of adaptation in coagulation and delivered a model that is both interpretable and practical for QSP applications.
Understanding AIDS treatment
Despite remarkable progress in HIV care, the virus remains stubbornly prevalent. Over 38 million people worldwide are living with HIV, and while antiretrovirals (ART) have transformed the prognosis, they are expensive, lifelong, and fraught with adherence and side-effect challenges. Enter broadly neutralizing antibodies (bNAbs), engineered to target HIV's most conserved regions with potent precision. In animal studies, especially SHIV-infected macaques and humanized mice, somewhere from 45% to 77% achieved durable viral suppression after receiving bNAbs (Nishimura et al. 2019, Nel & Frater 2024). This is a hopeful sign, but crucially, that means more than half to a quarter did not respond as well. That discrepancy has scientists asking: why do bNAbs shine in some cases but fall flat in others? Understanding the reasons behind this differential effectiveness is key to turning these powerful molecules into equitable, reliable treatments. This is a task that information geometry could help illuminate by pinpointing the underlying biological mechanisms at play.
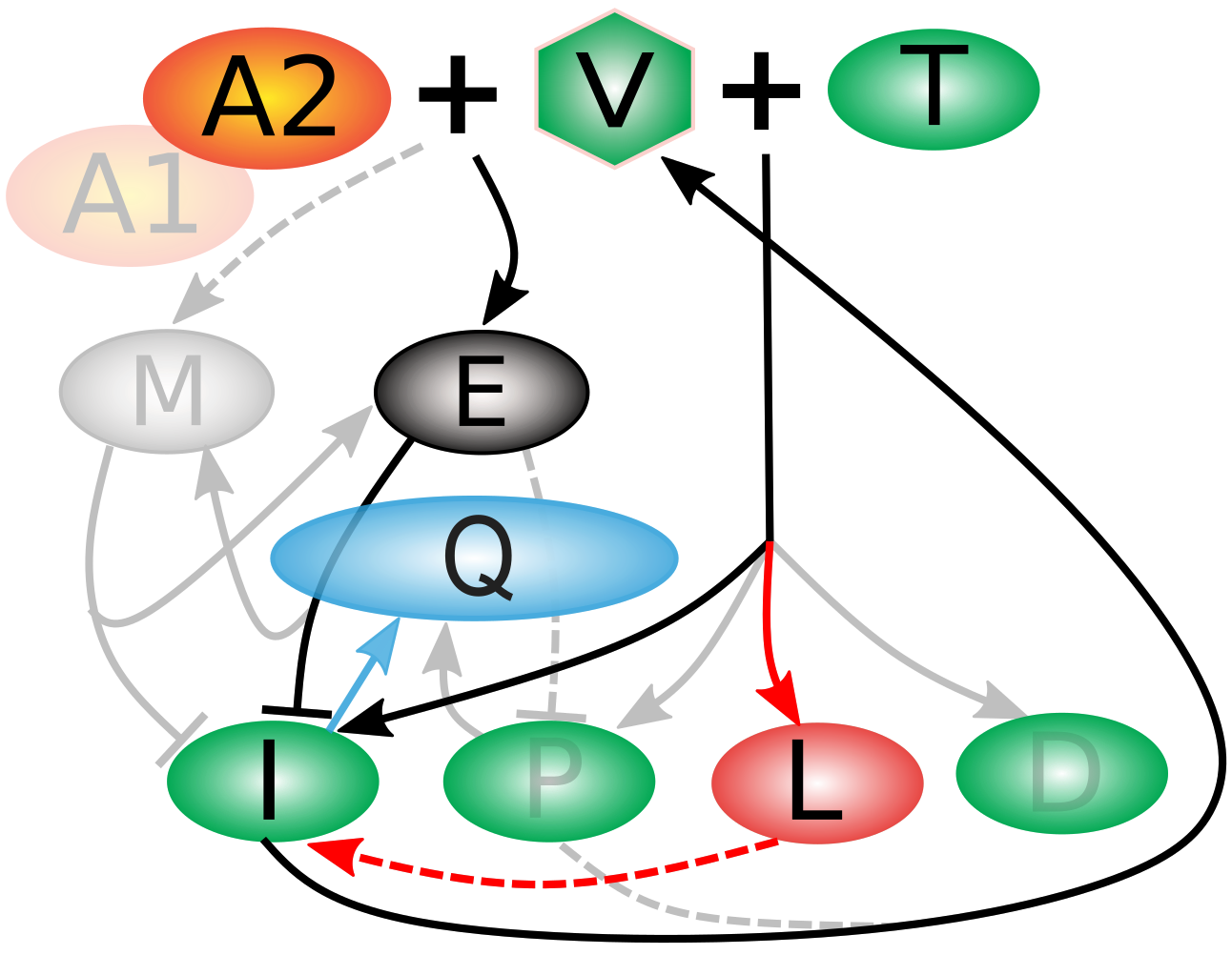
To examine this question, we built a model with 45 tunable parameters and 11 compartments by cobbling together classic models in the field (especially Desikan 2020, Funk 2001, and McLean 1994). Briefly, when a virus (V) encounters a helper T-cell (T), it creates one of four kinds of infected cells (bottom row) of which infected (I) and partially infected (P) cells produce more virus. However, when V encounters bNAb drugs A1 or A2, it activates effector cells (E) who work at efficiency Q to kill the I and P cells, and memory cells (M) to fight off later infection. Even when I and P are surpressed, latently infected cells (L) can reactivate, and some viral particles hang around in deficiently (D) infected cells.
| Schematic | FIM |
|---|---|
|
|
| Literature Derived Model | Relevon |
| $$ \begin{align*} \dot{T}&=b_T-d_T T-\left(f_I+f_L+f_P+f_D\right) T V \\ \dot{V}&=p_I I+p_P P-(c+A) V \\ \dot{I}&=f_I T V-d_I I+a L-m_I E I \\ \dot{L}&=f_L T V-d_L L-a L \\ \dot{P}&=f_P T V-d_P P-m_P E P \\ \dot{D}&=f_D T V-d_D D \\ \dot{E}&=\lambda _E+\frac{\left(I+f A V+\lambda _P P\right) \left(b_E+k_E E\right)}{K_B+\left(I+f A V+\lambda _P P\right)}-\xi\frac{ Q^n E}{q_c^n+Q^n}-d_E E \\ & \qquad +\lambda_M M \left(I+f_M A V+\lambda _{MP} P\right) \\ \dot{Q}&=\kappa \frac{I+\lambda _{QP} P}{\phi +I+\lambda _{QP} P}-d_Q Q \\ \dot{M}&=\left(\mu _M E+b_M \frac{\left(I+f A V+\lambda _P P\right) E}{K_B+\left(I+f A V+\lambda _P P\right)}\right) \left(1-\frac{M}{M_{\max }}\right) \\ A&=\frac{k_1 A_1+k_2 A_2}{K+A_1+A_2} \\ A_1& = \frac{A_1^{dose}}{Vol_1} \sum_i^3 e^{-\eta_1(t-(\tau_i+\omega_1))}H(t-(\tau_i+\omega_1))\\ A_2& = \frac{A_2^{dose}}{Vol_2} \sum_i^3 e^{-\eta_2(t-(\tau_i+\omega_2))}H(t-(\tau_i+\omega_2))\\ T(0)&=\frac{b_T}{d_T} \\ V(0)&=V_0 \end{align*} $$ | $$ \begin{align*} \dot{T}&=b_T-d_T T-\left(f_I+f_L\right) T V \\ \dot{V}&=p_I I-(c+A) V \\ \dot{I}&=f_I T V-d_I I+a L-\widetilde{E} I \\ \dot{L}&=f_L T V-a L \\ \dot{\widetilde{E}}&=\widetilde{\lambda_E}+\frac{I \left(\widetilde{b_E}+k_E \widetilde{E}\right)}{K_B+I} - \xi\frac{\widetilde{Q}^n \widetilde{E}}{1+\widetilde{Q}^n}-d_E \widetilde{E} \\ \dot{\widetilde{Q}}&=\widetilde{\kappa} \frac{I}{\phi +I}-d_Q \widetilde{Q} \\ A&=\frac{k_2 A_2}{K+A_1+A_2} \\ T(0)&=\frac{b_T}{d_T} \\ V(0)&=V_0 \end{align*} $$ |
A study at the NIH (Nishimura et al. 2019, which included Anthony Fauci as one of the authors) was able to provide a great deal of data on the time course of SHIV infection in monkeys treated with bNAbs, both responders and nonresponders. We used this information to fit the model, and then evaluate the Fisher Information Matrix at that point. As you can see from the eigenvalue spectrum, there were a large number of parameters in the red box that could be removed from the model (the greyed-out components of the model above), because they were many orders of magnitude less influential on the simulated time course of infection than those parameters we kept. We determined a 22-parameter model retained the flexibility to accurately predict daily viral load for two-and-a-half years for responders, nonresponders, untreated controls, and naturally immune patients alike.
What got cut out of the simplified models ("relevons") shed light on the puzzle of why bNAbs work remarkably well in some individuals but fail in others. By systematically simplifying detailed models, we found that nonresponders appear to harbor "hidden" viral reservoirs, especially latently infected cells, which act as a kind of viral safehouse (marked in red in the schematic above). In contrast, responders either avoid building these reservoirs or clear them effectively, but immune exhaustion (Q) is important to capturing the dynamics correctly in ways that were not important for nonresponders (marked in blue in the schematic above). This difference, revealed only when we distilled our models down to their most essential mechanisms, points toward new therapeutic strategies: if we can find ways to target or flush out latent cells, we may be able to convert nonresponders into responders. In this way, mathematical modeling not only explains why treatments succeed or fail but also helps chart a path toward more effective, personalized HIV therapies.
Information Geometry 101
When we talk about models, whether they describe molecules in a cell, financial markets, or climate systems, it's easy to get lost in equations and parameters. Information geometry offers a different lens: it treats families of models as geometric objects, with shapes, distances, and directions that capture how models relate to one another. That means we can ask questions like "Which models are nearly indistinguishable?" or "Which parameters really matter?" in a precise yet intuitive way. The beauty is that once you see models as living on a continuum from complex to simple (but physically interpretable at any level of complexity), a whole toolkit of geometric reasoning becomes available. We can then understand our system at a profound level, while comparing and predicting models with far more clarity than brute force alone.

Let's take a simple example to start with: $$ \dot{A} = w_1 B ~~~~~~ \dot{B} = w_2 C ~~~~~~ \dot{C} = w_3 A $$ This could represent any number of real physical systems: a rock-paper-scissors regulatory protein clique, or three cellular compartments sharing a metabolite in a loop. It doesn't even need to be biological; this system is a reasonable description of three connected electrical busses in a simple circuit. Pick whichever analogy is easiest for you to visualize.
The key first step is to understand that right now we have a three parameter system \({w_1, w_2, w_3}\). We have three state variables also (A, B, and C), but that isn't what matters right now. The process of model reduction asks the question, "What happens if we simplify the system by one parameter?" Generally speaking, we can do this by taking any of the parameters to either zero (which in this case corresponds to breaking a link) or infinity (fusing two of the proteins / compartments / busses).
In this case, if we go to infinity in the first step then a second weight parameter must also be dropped from the system, which violates the one step rule. For example, it is unclear if protein (AB) regulates C or vice versa. More clearly, some amount of metabolite / voltage is being shared between the (AB) and (C) compartments / busses, but that parameter describing that sharing is the only one left in the model. In all these cases, we have gone from three parameters to one in a single step, which is not allowed (at least for now).
So let's just consider what happens when we take parameters to zero in the first step. Taking \(w_1\rightarrow 0\) can be thought of as breaking the protein regulation clique, resulting instead in a regulation cascade where A regulates C at rate \(w_3\) and C in turn regulates B at rate \(w_2\) (but B no longer regulates A at all). Similarly, if we instead take \(w_2 \rightarrow 0\), then the resulting model says B -> A -> C, and so forth with \(w_3\).
The key takeaway is this: the three legal reductions leave us with three models of two parameters. All three state variables \(A,~B,~C\) are still present in all reduced models.
Now we can reduce any one of these three 2-parameter models further by taking one of the remaining weights to 0 as before, or increasing them to infinity, which essentially merges the compartments. This means there are technically four reductions available to each of the three models, but may of them result in the same reduced 1-parameter models, so we end up with six (not 12) unique 1-parameter models. Again, refer to the chart. Similarly, reducing this last parameter by either taking it to zero or infinity results in one of five possible 0-parameter models. All of these models are arranged below in what information theoreticians call a "Hasse Diagram", and each pathway from the initial 3-parameter model to the five possible 0-parameter models is called a "flag".
Here's where the Geometry part of Information Geometry comes in.
In practice, each of the three initial parameters \({w_1, w_2, w_3}\) has some value between 0 and infinity, and those three values can be thought of as a point in a three-dimensional "parameter space". The values of A, B, and C (and even their long term behavior) may be very different if the weights are {.1,.2,.1} than if they are {.5,1,2}, but those are just two different points in an 3-dimensional parameter space to a modeler, no matter what they make A, B and C do. So the full model can be thought of as defining a 3D space where each axis is one of the weight parameters. Similarly, each of the three 2-parameter models have a corresponding two-dimensional parameter space, and so on. This means we can think of the Hasse diagram for this example as a collection of:
- one 3D object (a polytope)
- three 2D faces each of which is bounded by four of the...
- six 1D edges (each edge is shared by exactly two of the 3D faces), and
- five zero-D vertices. Two of them are shared by three edges, and three are shared by two edges.
Count the grey arrows in the Hasse diagram above to confirm. Though this object might be a bit difficult to picture, such a polytope does exist, and looks something like the 3d model.
Information geometry imagines the process of reducing a model as traveling from a point on the interior of the polytope to a face, then an edge, and finally to a vertex. These could be extremely poor approximations to real data. For example, the vertex (A)(B)(C) might be a good fit if the connections between the compartments are extremely weak, but a terrible approximation if they are strong. In our experience, applying this method hundreds of times to a wide variety of problems from many domains of knowledge, it is generally the case that at least a few rounds of reductions on high-dimensional real world models preserve prediction fidelity. This is because almost all real world models (and the phenomena they model) are "sloppy": that is, you can travel a very long way in some directions of parameter space while barely changing the data at all; conversely, there are a few "stiff" directions that will have an effect on your data many orders of magnitude larger. At any given point in parameter space, it is possible to map exactly how much your data will change if you walk one unit in a given direction in parameter space. This map is called the Fisher Information Matrix. This is the primary tool of Information Geometry, since it tells you which directions are "safe" to travel in until you reach an extreme value; in other words, which parameters can be removed to produce a reduced model that fits your data just as well as the original.
If you'd like to see this process in action, take a look at this prototype demo. Be aware this is very much still under construction, but gives you some idea of what one step of reductions looks like for any simple system.
MBAM one-step Demo (Under construction)
Are you ready to find your revelon?
Let us help you deeply understand your system as well! Contact Us!
